Расчет основных параметров системы индуктор-деталь индукционной установки

1. Расчет параметров системы индуктор-деталь

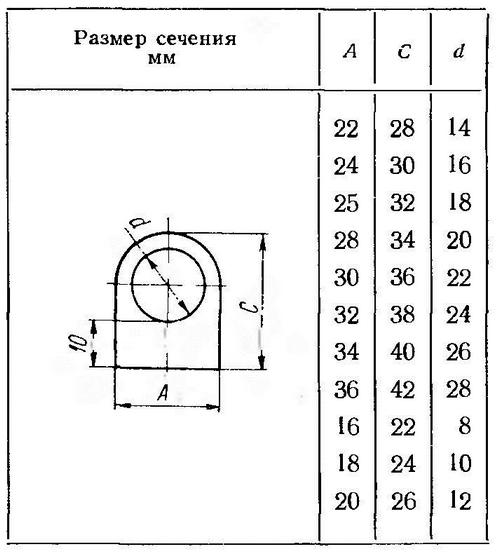
Основной задачей расчета электромагнитной системы для ин­дукционного нагрева является определение входных параметров нагруженного индуктора: активного и реактивного сопротивлений, к. п. д., коэффициента мощности, тока, напряжения и числа витков по заданным геометрическим размерам (рис. 12), частоте тока, мощности и электрическим свойствам материала индуктора и де­тали. Поскольку индуктор и деталь образуют систему с распре­деленными параметрами, понятия сопротивлений не являются однозначно определенными, а обязательно относятся к схеме за­мещения, представляющей собой электрическую цепь, которой заменяется нагруженный индуктор. Каждое сопротивление харак­теризует активную или реактивную мощность в том или ином объеме реальной системы. В расчетах используется обычно два вида сопротивлений. Если разделить мощность в детали (Р_а или Р_р) на (Н₀l)², то получим сопротивления детали (r₂ и х_2м), приведен­ные (отнесенные) к намагничивающему току на ее поверхности (I_н= Н₀l). Эти сопротивления иногда неточно называют собственными. Если вместо I_н взять ток индуктора I_и, то получим приведенные к индуктору (или вносимые) сопротивления r₂' и х_2м'. Для активного сопротивления детали

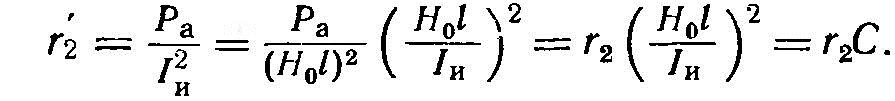
В результате расчета нужно найти вносимые сопротивления r₂' и х_2м'. Сопротивления r₂ и х_2м являются промежуточными и опре­деляются по приведенным ранее формулам для Р_а и Р_р.

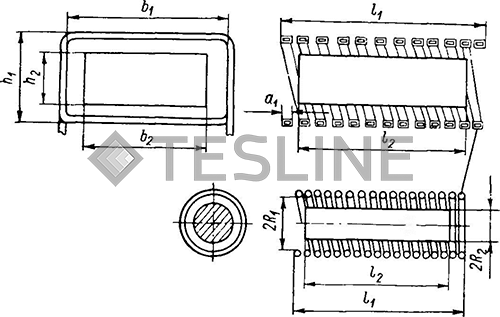
Рис. 12. Геометрические размеры системы индуктор-деталь

Величина С называется коэффициентом приведения параметров и характеризует длину системы. Коэффициент приведения всегда меньше единицы и лишь при большой длине системы (l₁ >> 2R₁и l₁ = l₂) стремится к ней.

Приведенные рассуждения справедливы лишь при условии, что магнитное поле на поверхности детали однородно (H₀= const). Это допущение принимается при всех приближенных расчетах. Лишь в последнее время появились расчеты по методу наведен­ных э. д. с., в которых неоднородность поля учитывается заранее. Эти расчеты дают точные результаты, однако они раз­работаны только для простых индукционных систем.

Во всех приближенных методах сначала определяются вели­чины r и х_2м, которые затем пересчитываются в r₂' и  х_2м', т. е. приводятся к току индуктора. Существующие методы отличаются только способами приведения сопротивлений детали. Из них наи­более распространены три метода - метод связанных контуров, поправочных коэффициентов и метод общего потока. При любом способе расчета предварительно определяются параметры пустого индуктора - r₁ и х₁.

Сопротивления пустого индуктора. Если специально не огово­рено, то принимается, что индуктор изготовлен в виде однослойной катушки из медной трубки. Для индукторов следует исполь­зовать только электротехническую медь марок М0 или Ml, так как наличие нежелательных добавок, например фосфора, резко увеличивает ее удельное сопротивление. При рабочей темпера­туре (20÷50) °С сопротивление меди Ml можно считать ρ = (1,8ч2) 10^-6 Ом см. Трубка индуктора обычно профилируется на прямоугольник. Принято считать, что в наружных индукторах основная часть тока протекает по стенке трубки, обращенной в сторону детали.

Тогда для индуктора длиной l₁ из w витков трубки с толщиной стенки т₁ (см) активное сопротивление равно

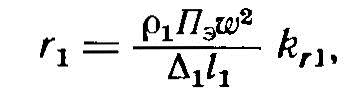
где Δ₁ -глубина проникновения тока в медь; П_э- эквивалентный периметр окна индуктора:

для цилиндрического индуктора с внутренним радиусом R₁  П_э = 2 πR₁, для прямоугольного индуктора с окном h₁ х b₁  П_э = 2 (h_t + b₁ + 2Δ).

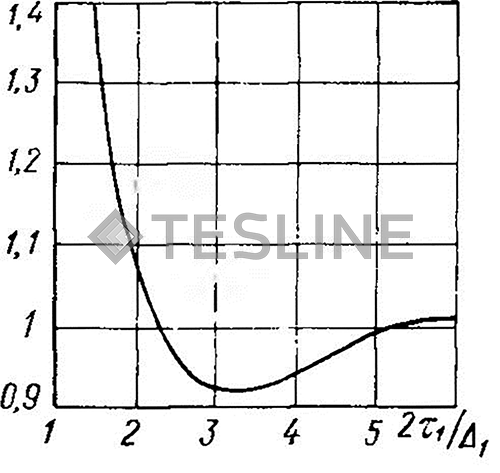
Рис. 13. Значения k_r1

Коэффициент увеличения сопротивления k_r1 учитывает тол­щину стенки трубки (рис. 13). Его минимальная величина, равная 0,92, соответствует 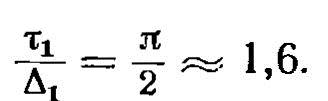 Поскольку минимальному r₁ соответствуют минимальные потери тепла, толщину трубки сле­дует брать в пределах τ₁ = (1,25÷2,8) Δ₁ (табл. 11).

 

Таблица 11. Оптимальная и предельная толщина трубки индуктора

Для индукторов промышленной частоты изготовляются спе­циальные неравностенные трубки (табл. 12).

 

Таблица 12. Сложные профили токопроводов для индукторов промышленной частоты тока

Иногда для этой цели используют равностенные трубки толщиной τ₁ = (З÷4) мм. По­скольку на частоте 50 Гц Δ₁ = 10 мм и поверхностный эффект в проводе выражен слабо, для однослойных обмоток r₁ (Ом) можно определять, как на постоянном токе:

где S₀-площадь поперечного сечения меди проводника.

В формуле для r₁ на повышенной частоте обычно в знаменатель вводится величина g - коэффициент заполнения индуктора медью по длине. Изучение распределения плотности то­ка и потерь в проводни­ках в зависимости от фор­мы трубки и зазора между витками показало, что r₁ на повышенных частотах слабо зависит от g в обычно исполь­зуемом диапазоне (0,6 ≤ g ≤ 0,9). Поэтому коэффициент g из формулы исключен. Форма проводника (прямо­угольная или круглая труб­ка) также не дает существен­ных различий в r₁, однако прямоугольное сечение обес­печивает большую площадь окна для охлаждающей воды при том же коэффициенте g.

Расчетные формулы для цилиндрического индуктора:

Аналогично для индуктора прямоугольного сечения высотой окна h₁, шириной b₁ и длиной l₁

 

Реактивное сопротивление индуктора определяется по извест­ной формуле:

где ω = 2πf - круговая частота; S₁- площадь окна индуктора, ограниченная эквивалентным периметром, см²; k_x1 - поправоч­ный коэффициент самоиндукции, зависящий от длины индуктора (рис. 14).

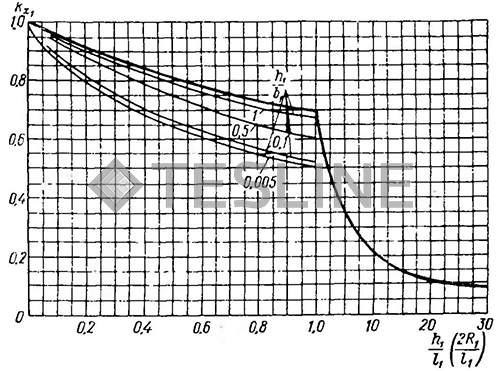
Рис. 14. Значения k_x1: - для цилиндров; - - для индук­торов прямоугольного сечения 

Расчетная формула для цилиндрического индуктора:

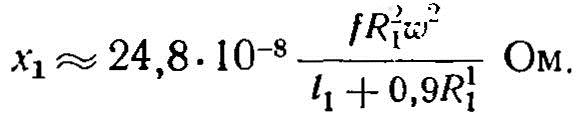
Здесь принято

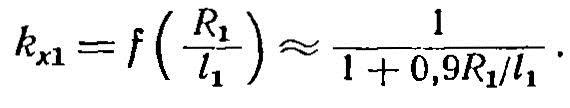
Для индуктора прямоугольного сечения

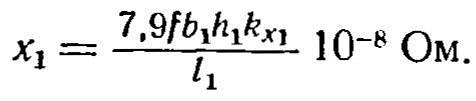
Рассмотрим основные методы расчета вносимых сопротивлений детали.

Метод связанных контуров. Метод основан на аналогии индук­тора и детали с двумя связанными катушками. Вторичная ка­тушка, заменяющая деталь и имеющая один виток с радиусом R₂ и длиной l₂, замкнута на сопротивление r₂, определенное для отрезка длинного индуктора. Конечная длина индуктора и детали учитывается поправочными коэффициентами. Полное сопротивле­ние индуктора

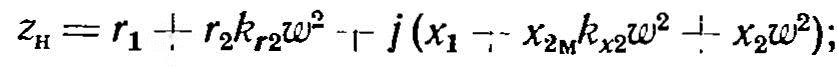
здесь k_r2 и k_х2 - поправочные коэффициенты активного и ре­активного сопротивлений детали (рис. 15, 16); х_2м- индуктив­ное сопротивление потоку внутри детали;

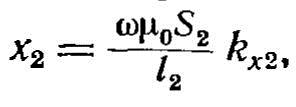
где S₂- площадь сечения детали по внешнему периметру.

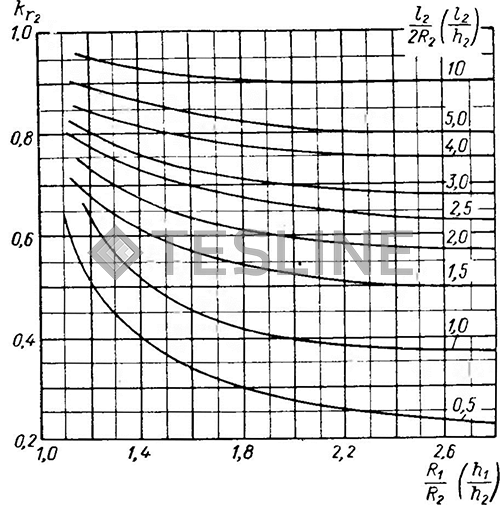
Рис. 15. Значения k_r2

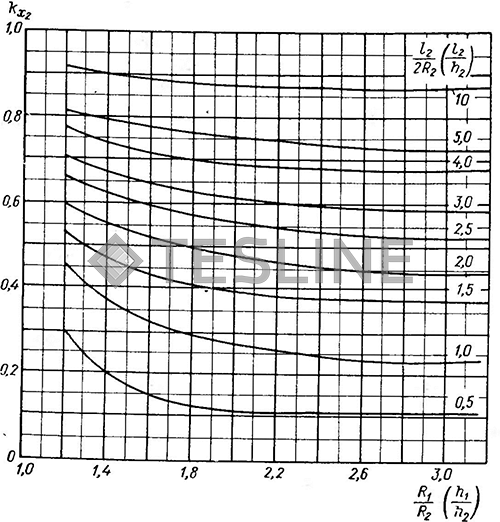
Рис. 16. Зна­чения k_x2

Для цилиндрических деталей

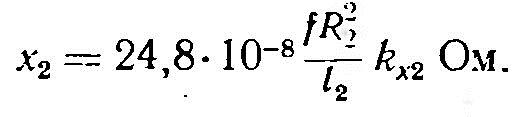
Коэффициенты k_r2 и k_x2 зависят только от геометрических размеров индуктора и детали:

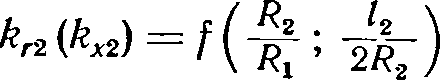
и применимы лишь при l₂ ≈ l₁. При нагреве прямоугольных тел вместо R₁ и R₂ следует брать 2h₁ и 2h₂. Метод не является универ­сальным, так как k_r2 и k_x2 не зависят от частоты тока и свойств нагреваемой детали. Однако он является самым простым и может применяться для индукторов большой длины (l₁ > 5R₁).

Метод расчета по общему потоку. Метод основан на составлении и расчете магнитной схемы замещения нагруженного индуктора. Допускается, что все его витки охвачены одним общим потоком. Участок прохождения магнитного потока по детали и по зазору вдоль ее поверхности является полезным и рабочим, а участок внутри индуктора, но вне детали (при l₁ > l₂) и снаружи индуктора - участком замыкания потока. Сопротивления, обусловленные наличием зазора (x_s) и детали (r₂ и х_2м), рассчитываются как для отрезка длиной l₂ бесконеч­ной системы (еслиl₂ > l₁, то условно считаем l₂ =- l₁). Расчет прост и универсален. Ошибка расчета обычно не превышает 8% по х_н и 10-15% по r_н.

 

Полное сопротивление индуктора равно

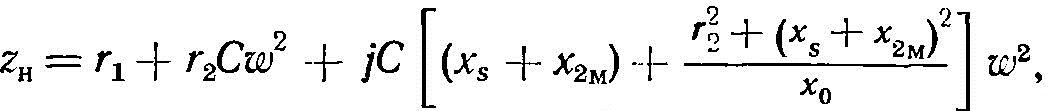
где х₀ - сопротивление обратного замыкания; С - коэффициент приведения параметров;

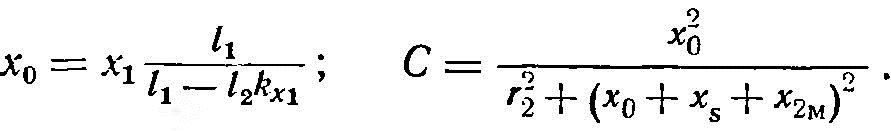
Формулы для расчета r₂, х_2м, х₀ и x_s сведены в табл. 13.

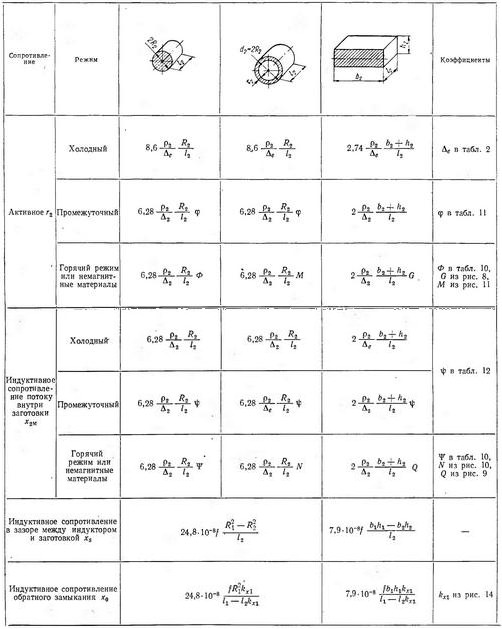
Таблица 13. Формулы для определения активных и реактивных сопротивлений нагреваемых тел различной формы

 

Порядок электрического расчета индуктора следующий.

1. По электрическим свойствам определяем глубины проник­новения:

 

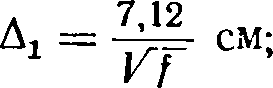
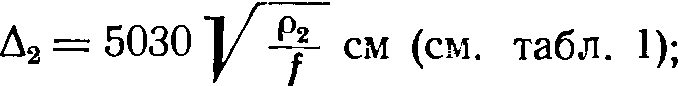
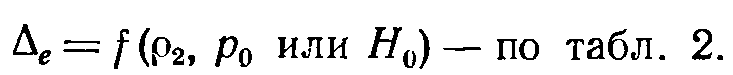
Если ρ₂ > 18∙10 ⁶, то полученное Δ_е нужно увеличить в 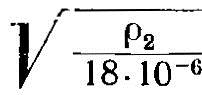 раз.

2. Находим расчетные геометрические размеры индуктора и детали в каждом режиме в соответствии с табл. 13. В горячем режиме расчетные размеры детали равны истинным.

3. По формулам табл. 13 рассчитываем сопротивления r₂, х_2м и x_s и вычисляем коэффициент С.

4. Находим активное сопротивление пустого индуктора r₁.

5. Сопротивления нагруженного индуктора:

 

 

 

 

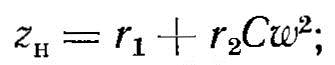
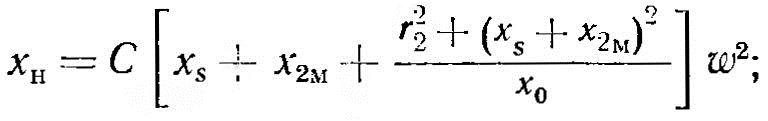
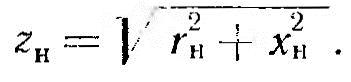
6. Электрический к. п. д.

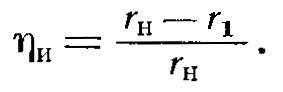
7. Коэффициент мощности

 

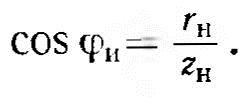
8. Активная и реактивная мощности индуктора:

 

 

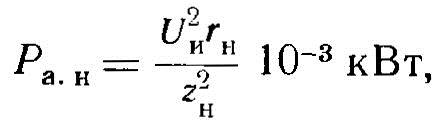
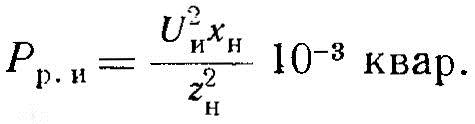
9. Ток индуктора

 

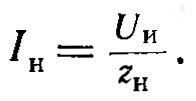
10. Число витков. Если число витков заранее неизвестно, в расчете полагаем w - 1 и затем число витков находим по фор­муле

 

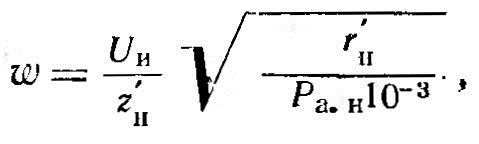
где Р_а.н - мощность в кВт; z_н' и r_н' - сопротивления при w = 1.

 

11. Пересчет индуктора. Индуктор будет потреблять мощ­ность Р'_{а. и} вместо Р_{а. и} при том же напряжении, если изменить число витков

 

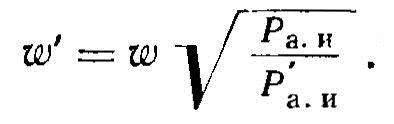
Индуктор с числом витков w' вместо w будет потреблять ту же мощность, если на нем изменить напряжение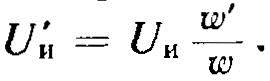 

 

2. Выбор частоты и размеров индуктора

Выбор частоты является одним из наиболее ответственных мо­ментов при проектировании индукционных установок. Он опре­деляется требованием высокого электрического к. п. д. как индук­тора, так и всей установки, необходимостью получения заданного распределения температуры по сечению детали, наличием и тех­ническими данными оборудования (преобразователей требуемой мощности, конденсаторов, контакторов). Окончательно частота выбирается по результатам технико-экономического анализа.

Однако основные требования к частоте определяются системой индуктор-деталь. При поверхностной закалке для получения высокого термического к. п. д. и хорошего качества термообра­ботки необходимо обеспечить так называемый глубинный тип нагрева, при котором горячая глубина проникновения тока Δ₂ в один-три раза превышает толщину нагреваемого под закалку слоя. Отсюда рекомендуемый диапазон частот равен

 

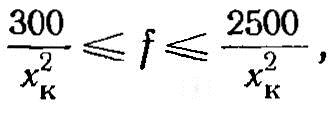
где х_к - глубина закаленного слоя в см.

При сквозном нагреве противоположные требования предъяв­ляют условия равномерного нагрева по всему сечению и высокого электрического к. п. д. При понижении частоты равномерность нагрева повышается, т. е. время нагрева может быть сокращено. Однако, начиная с некоторой частоты, распределение мощности ста­новится постоянным, при этом время нагрева является минимально возможным. Для сплошных тел (круглого и прямоугольного се­чений) при переходе от низкой частоты к высокой, при которой вся мощность выделяется в тонком поверхностном слое, время нагрева увеличивается примерно в 1,8-2 раза при той же равно­мерности нагрева.

Зависимость электрического к. п. д. от частоты довольно сложна и определяется характером детали и ее состоянием. Для сплош­ных деталей (круглых и прямоугольных) к. п. д. обычно растет с повышением частоты, стремясь к предельному значению. Для полых цилиндров и широких пластин существует оптимальная частота, при которой к. п. д. максимален. При нагреве ферро­магнитных тел к. п. д. зависит от частоты косвенно, через μ_е. Одна и та же удельная мощность будет передаваться на более вы­сокой частоте при меньших напряженностях Н₀. Это приведет к росту μ_е, и, следовательно, повышению r₂ и η_и.

Используя полученные ранее формулы для η_и, можно написать выражение

 

где ϒ - один из коэффициентов (φ, Ф, М, G), относящийся к дан­ному режиму и виду детали.

В приведенной формуле от частоты зависят k_r1, μ₂ (при по­стоянстве р₀), С и ϒ. Поскольку k_r1 всегда может быть взято близким к оптимуму, а С мало за­висит от f, частотная зависимость η_и определяется в основном коэффи­циентом ϒ. Наибольшему значению ϒ соответствует максимум η_и: При по­вышении частоты ϒ стремится к еди­нице и к. п. д. достигает своего пре­дельного значения

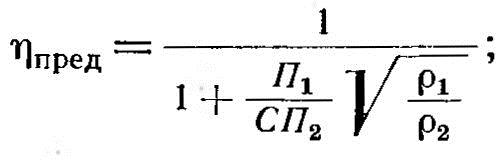
здесь μ₂ равна единице.

Предельный к. п. д. зависит только от геометрических размеров системы и удельного сопротивления р₂.

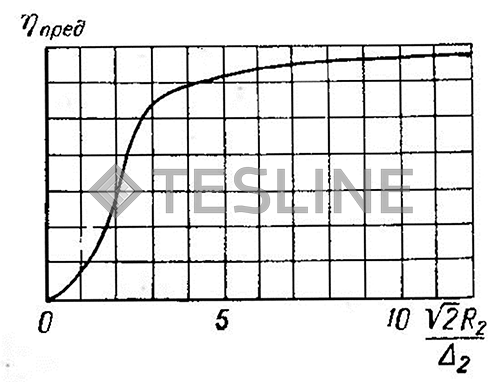
Рис. 17. К. п. д. индуктора при нагреве сплошного цилиндра

Сплошной цилиндр радиусом R₂. При μ₂ = 1 и ϒ = Ф частотная зависимость η_и определяется видом функции Ф = f (f) (см. табл. 10). Качественный характер кривой η_и = f (т) приведен на рис. 17. Из рисунка следует, что к. п. д. приближается к предельному уже при 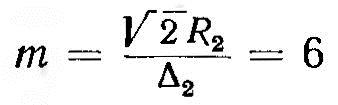 или R₂ > 4Δ₂, при т < 2,5 резко па­дает. Оптимальным можно считать диапазон 2,5 ≤ т ≤ 5, в ко­тором к. п. д. остается близким к предельному при удовлетвори­тельной равномерности нагрева. Отсюда частота для нагрева стальных деталей (ρ = 10^-4 Ом∙см) равна

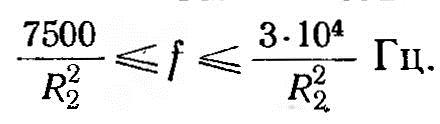
При отсутствии подходящего оборудования в этом диапазоне частоту следует брать выше, одновременно увеличивая время на­грева.

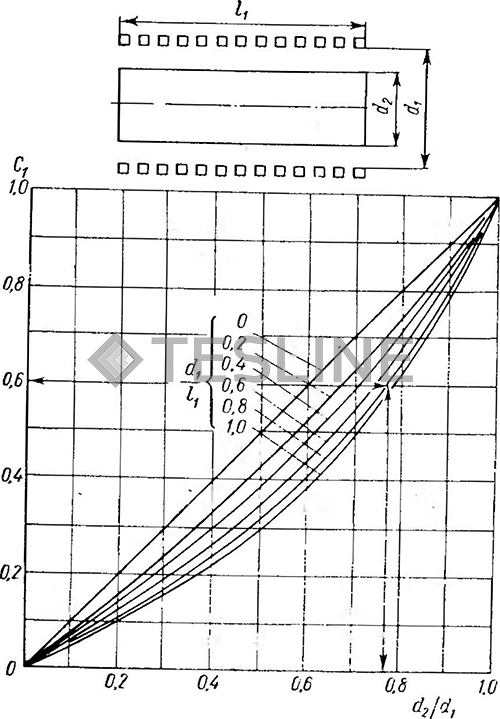
Рис. 18. Вспомога­тельная величина С₁

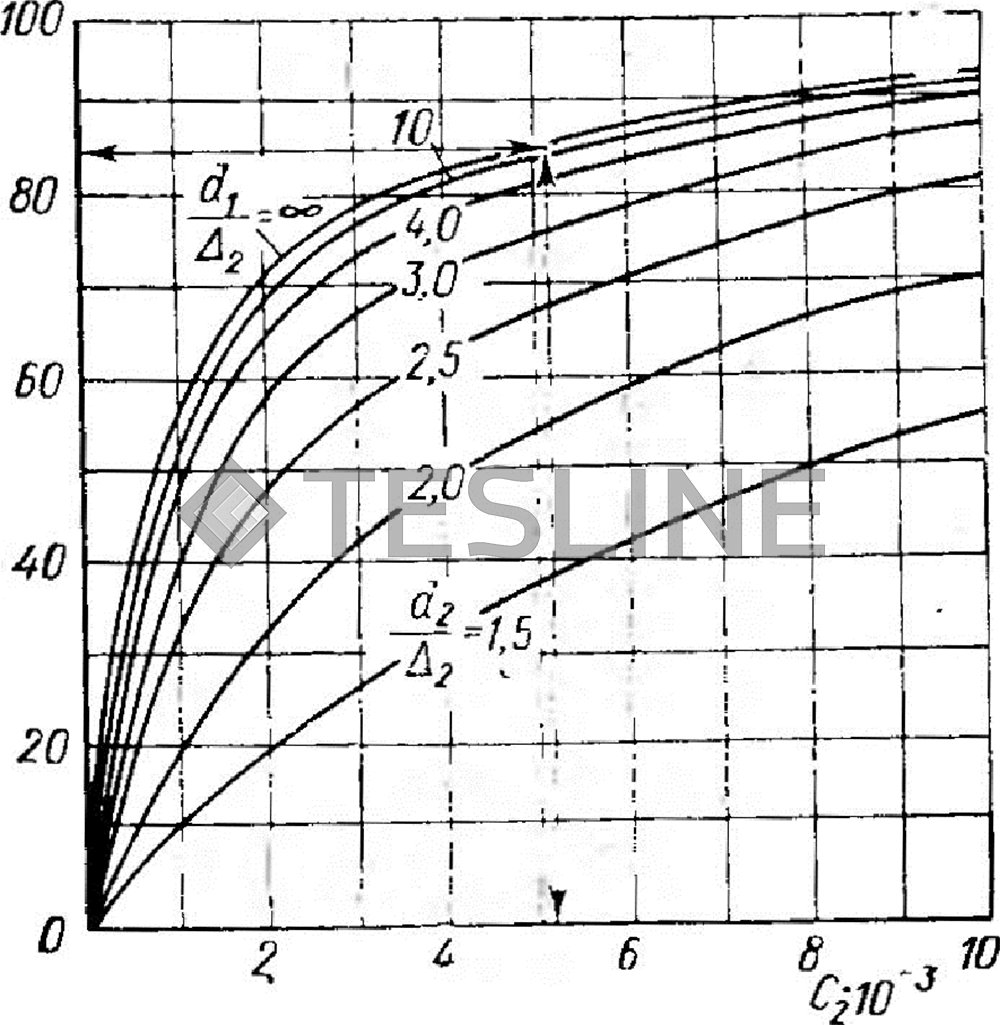
Рис. 19. Кпд системы индук­тор-деталь в зависимости от С₂=С₁ √ρμ 

К. п. д. индуктора, длина которого больше диаметра, можно вычислить достаточно точно, пользуясь графиками рис. 18 и 19. Для этого следует проделать следующее:

найти отношение диаметра проводника к внутреннему диа­метру индуктора d₂/d₁;

определить отношение внутреннего диаметра индуктора к его длине d₂/l₁;

вычислить квадратный корень из произведения электрического сопротивления проводника на его относительную магнитную про­ницаемость (√ρ₂μ₂);

найти отношение диаметра проводника к глубине проникнове­ния тока (d₂/Δ₂);

по кривым графика рис. 18 найти вспомогательную величину С₁; вычислить вспомогательную величину С₂ = С₁ √ρ₂μ₂;

по графику на рис. 19 найти к. п. д. индуктора.

При уменьшении длины индуктора к. п. д. снижается из-за уменьшения коэффициента приведения С.

Из графика следует, что увеличение зазора приводит к за­метному снижению к. п. д., особенно при низкой частоте (m < 2,5). Кроме того, сильно падает коэффициент мощности индуктора и увеличивается конденсаторная батарея.

Явление резкого падения к. п. д. индуктора при т < 2,5 мо­жет быть использовано на практике для выравнивания темпера­туры неравномерно нагретой по длине заготовки из ферромагнит­ных материалов с последующим догревом на более высокой частоте или в случае, когда требуется нагрев только до температуры точки Кюри без опасения перегрева. Для этого частоту подбирают так, чтобы в горячем режиме глубина проникновения не превы­шала радиус детали. В холодном режиме μ_е велико и нагрев происходит интенсивно. С потерей магнитных свойств т снижается (т < 1,4) и нагрев практически прекращается. Этот способ ста­билизации температуры требует осторожности, так как при пере­ходе в горячий режим ток индуктора может сильно возрасти из-за падения z_и, и мощность, потребляемая индуктором, снизится мало при резком увеличении потерь в индуктирующем проводе.

На рис. 20 показан максимально возможный к. п. д. при на­греве немагнитных материалов с разными значениями электро­сопротивления. Предполагается, что d₂/Δ₂ = ∞.

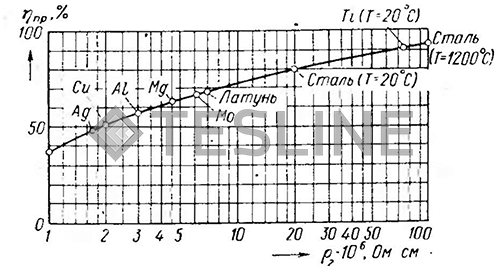
Рис. 20. Максимальный к.п.д. индуктора при на­греве материалов с различными значениями ρ. Для стали при μ =1 

Заготовки прямоугольного сечения. Так как ϒ = G, то зависи­мость к. п. д. от частоты можно проследить по рис. 8. Для широких пластин (b₂/h₂ → ∞) максимум к. п. д. соответствует h₂ = πΔ₂, т. е. частоте f = 8,1∙10⁶ ρ₂h₂². Нагрев квадратных заготовок аналогичен нагреву цилиндра с той же площадью сечения. К. п. д. индукторов для нагрева прямоугольных тел обычно выше, чем цилиндриче­ских, не только за счет различия коэффициентов G и Ф, но и из-за лучшего соотношения периметров деталей и индукторов.

Полый цилиндр с наружным радиусом R₂ и толщиной стенки т₂. К. п. д. длинного индуктора определяется формулой

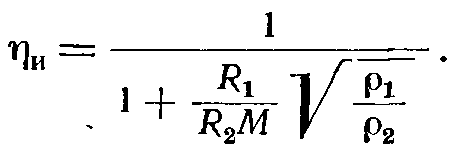
Для полых цилиндров, в отличие от сплошных, имеется опти­мальная частота, при которой к. п. д. максимален. Этот максимум заметно выражен лишь при малых толщинах стенки (т₂ ≤ 0,2R₂):

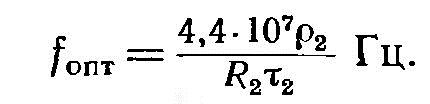
Максимум к. п. д. является пологим, и возможны значитель­ные отклонения от оптимальной частоты без заметного падения к. п. д., и можно рекомендовать следующие пределы:

 

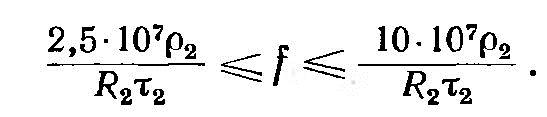
Уменьшение частоты приводит к резкому падению к. п. д. С увеличением частоты выше указанного диапазона к. п. д. падает до минимума при т₂ = π/2 Δ₂ и затем немного снова поднимается, стремясь к предельному значению для сплошного цилиндра.

Для коротких индукторов (l₁ < 4R₁) при нагреве деталей всех видов желательно увеличение частоты по сравнению с реко­мендованной. Это увеличение может достигать полуторакратной величины.

Например, при нагреве полых цилиндров в коротких индук­торах (l₁ < 2R₁) частоту следует брать в диапазоне

---

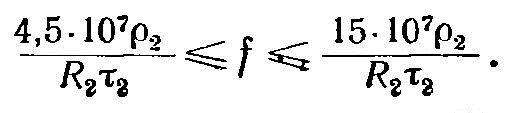
Источник: "Проектирование и эксплуатация высокочастотных установок" Шамов А. Н., Бодажков В. А.